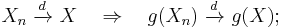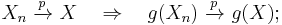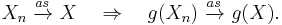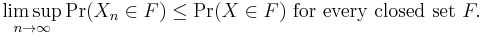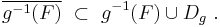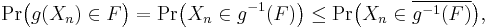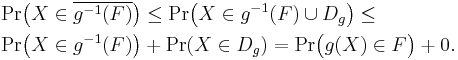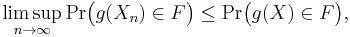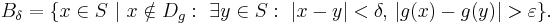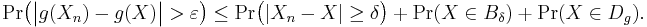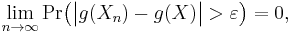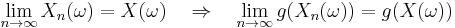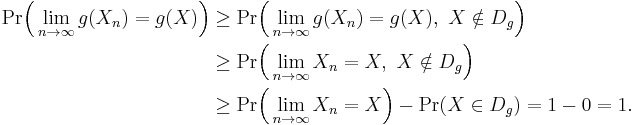Continuous mapping theorem

In probability theory, the continuous mapping theorem states that continuous functions are limit-preserving even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if xn → x then g(xn) → g(x). The continuous mapping theorem states that this will also be true if we replace the deterministic sequence {xn} with a sequence of random variables {Xn}, and replace the standard notion of convergence of real numbers “→” with one of the types of convergence of random variables.

This theorem was first proved by (Mann & Wald 1943), and it is therefore sometimes called the Mann–Wald theorem.[1]

Contents

Statement

Let {Xn}, X be random elements defined on a metric space S. Suppose a function g: S→S′ (where S′ is another metric space) has the set of discontinuity points Dg such that Pr[X ∈ Dg] = 0. Then[2][3][4]

  1. X_n \ \xrightarrow{d}\ X \quad\Rightarrow\quad g(X_n)\ \xrightarrow{d}\ g(X);
  2. X_n \ \xrightarrow{p}\ X \quad\Rightarrow\quad g(X_n)\ \xrightarrow{p}\ g(X);
  3. X_n \ \xrightarrow{\!\!as\!\!}\ X \quad\Rightarrow\quad g(X_n)\ \xrightarrow{\!\!as\!\!}\ g(X).

Proof

This proof has been adopted from (van der Vaart 1998, Theorem 2.3)

Spaces S and S′ are equipped with certain metrics. For simplicity we will denote both of these metrics using the |x−y| notation, even though the metrics may be arbitrary and not necessarily Euclidian.

Convergence in distribution

We will need a particular statement from the portmanteau theorem: that convergence in distribution 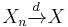X_n\xrightarrow{d}X is equivalent to

\limsup_{n\to\infty}\operatorname{Pr}(X_n \in F) \leq \operatorname{Pr}(X\in F) \text{ for every closed set } F.

Fix an arbitrary closed set F⊂S′. Denote by g−1(F) the pre-image of F under the mapping g: the set of all points x∈S such that g(x)∈F. Consider a sequence {xk} such that g(xk)∈F and xk→x. Then this sequence lies in g−1(F), and its limit point x belongs to the closure of this set, g−1(F) (by definition of the closure). The point x may be either:

Thus the following relationship holds:

\overline{g^{-1}(F)} \ \subset\ g^{-1}(F) \cup D_g\ .

Consider the event {g(Xn)∈F}. The probability of this event can be estimated as

\operatorname{Pr}\big(g(X_n)\in F\big) = \operatorname{Pr}\big(X_n\in g^{-1}(F)\big) \leq \operatorname{Pr}\big(X_n\in \overline{g^{-1}(F)}\big),

and by the portmanteau theorem the limsup of the last expression is less than or equal to Pr(X∈g−1(F)). Using the formula we derived in the previous paragraph, this can be written as

\begin{align} & \operatorname{Pr}\big(X\in \overline{g^{-1}(F)}\big) \leq \operatorname{Pr}\big(X\in g^{-1}(F)\cup D_g\big) \leq \\ & \operatorname{Pr}\big(X \in g^{-1}(F)\big) %2B \operatorname{Pr}(X\in D_g) = \operatorname{Pr}\big(g(X) \in F\big) %2B 0. \end{align}

On plugging this back into the original expression, it can be seen that

\limsup_{n\to\infty} \operatorname{Pr}\big(g(X_n)\in F\big) \leq \operatorname{Pr}\big(g(X) \in F\big),

which, by the portmanteau theorem, implies that g(Xn) converges to g(X) in distribution.

Convergence in probability

Fix an arbitrary ε>0. Then for any δ>0 consider the set Bδ defined as

B_\delta = \big\{x\in S\ \big|\ x\notin D_g:\ \exists y\in S:\ |x-y|<\delta,\, |g(x)-g(y)|>\varepsilon\big\}.

This is the set of continuity points x of the function g(·) for which it is possible to find, within the δ-neighborhood of x, a point which maps outside the ε-neighborhood of g(x). By definition of continuity, this set shrinks as δ goes to zero, so that limδ→0Bδ = ∅.

Now suppose that |g(X) − g(Xn)| > ε. This implies that at least one of the following is true: either |X−Xn|≥δ, or X∈Dg, or X∈Bδ. In terms of probabilities this can be written as

\operatorname{Pr}\big(\big|g(X_n)-g(X)\big|>\varepsilon\big) \leq \operatorname{Pr}\big(|X_n-X|\geq\delta\big) %2B \operatorname{Pr}(X\in B_\delta) %2B \operatorname{Pr}(X\in D_g).

On the right-hand side, the first term converges to zero as n → ∞ for any fixed δ, by the definition of convergence in probability of the sequence {Xn}. The second term converges to zero as δ → 0, since the set Bδ shrinks to an empty set. And the last term is identically equal to zero by assumption of the theorem. Therefore the conclusion is that

\lim_{n\to\infty}\operatorname{Pr}\big(\big|g(X_n)-g(X)\big|>\varepsilon\big) = 0,

which means that g(Xn) converges to g(X) in probability.

Convergence almost surely

By definition of the continuity of the function g(·),

\lim_{n\to\infty}X_n(\omega) = X(\omega) \quad\Rightarrow\quad \lim_{n\to\infty}g(X_n(\omega)) = g(X(\omega))

at each point X(ω) where g(·) is continuous. Therefore

\begin{align} \operatorname{Pr}\Big(\lim_{n\to\infty}g(X_n) = g(X)\Big) &\geq \operatorname{Pr}\Big(\lim_{n\to\infty}g(X_n) = g(X),\ X\notin D_g\Big) \\ &\geq \operatorname{Pr}\Big(\lim_{n\to\infty}X_n = X,\ X\notin D_g\Big) \\ &\geq \operatorname{Pr}\Big(\lim_{n\to\infty}X_n = X\Big) - \operatorname{Pr}(X\in D_g) = 1-0 = 1. \end{align}

By definition, we conclude that g(Xn) converges to g(X) almost surely.

See also

References

Literature

  • Amemiya, Takeshi (1985). Advanced Econometrics. Cambridge, MA: Harvard University Press. ISBN 0674005600. LCCN 1985 HB139.A54 1985. 
  • Billingsley, Patrick (1969). Convergence of Probability Measures. John Wiley & Sons. ISBN 0471072427. 
  • Billingsley, Patrick (1999). Convergence of Probability Measures (2nd ed.). John Wiley & Sons. ISBN 0471197459. 
  • Mann, H.B.; Wald, A. (1943). "On stochastic limit and order relationships". The Annals of Mathematical Statistics 14 (3): 217–226. doi:10.1214/aoms/1177731415. JSTOR 2235800. 
  • Van der Vaart, A. W. (1998). Asymptotic statistics. New York: Cambridge University Press. ISBN 9780521496032. LCCN .V22 1998 QA276 .V22 1998. 

Notes

  1. ^ Amemiya 1985, p. 88
  2. ^ Van der Vaart 1998, Theorem 2.3, page 7
  3. ^ Billingsley 1969, p. 31, Corollary 1
  4. ^ Billingsley 1999, p. 21, Theorem 2.7